Zur Zitation: W. Fuhrmann, A. Sultanow (2002), Der gesamtwirtschaftliche Arbeitsmarkt; in:
www.nowgorod.de, Stand : 2002-02-03
Inhalt
1. Zur
Arbeitsmarktkonstellation 2
2. Die
Produktionsfunktion 3
2.1. Zur
substitutionalen Produktionsfunktion 3
2.1.1. Zur Cobb-Douglas-Produktionsfunktion 5
2.2. Zur limitationalen Produktionsfunktion
(Leontief-Produktionsfunktion) 7
3. Der
Arbeitsmarkt bei Mengenanpasserverhalten 8
3.1. Die
Arbeitsnachfrage 8
3.2. Das Arbeitsangebot 11
3.3. Angebot und Nachfrage auf dem Arbeitsmarkt 16
1. Zur
Arbeitsmarktkonstellation
Aus makroökonomischer Sicht agieren auf dem
Arbeitsmarkt einerseits Unternehmen als Güteranbieter und
Arbeitskraftnachfrager, anderseits Haushalte als Güternachfrager und
Arbeitskraftanbieter.
Die
Situation auf dem Arbeitsmarkt wird hier durch Annahmen aus dem Gütermarkt über
die stets vollständige Anpassung des Angebots an die Nachfrage bei gegebenen
Preisen, also einen konstanten Zinssatz, Güterpreis und Lohnsatz sowie bei
einem konstanten Kapitalstock (außer bei der Analyse des Akzeleratorprinzips
und seinen Auswirkungen) und einem konstanten Vermögen, bestimmt. Es bedeutet
die Möglichkeit, die für zusätzliche Produktion notwendigen Arbeitskräfte auf
dem Arbetsmark finden und im
Produktionsprozeß einzusetzen zu können.
Eine solche
Situation charakterisiert ein kurzfristiges Gleichgewicht mit konjunktureller
unfreiwilliger Arbeitslosigkeit, bei dem die Produzenten zum herrschenden
Güterpreis jede gewünschte Gütermenge und die Arbeitnehmer zum exogen gegebenen
Nominallohnsatz jede nachgefragte Arbeitsmenge anzubieten bereit sind.
Im
folgenden wird während der Analyse des Zusammenhangs zwischen Arbeitsmarkt und Güterangebot unterstellt, daß der
Produktionsfaktor Arbeit vollkommen homogen ist und eine gegebene
(gesamtwirtschaftliche) Produktionsfunktion existiert. Die Annahme der
Homogenität des Produktionsfaktors Arbeit bedeutet, daß die Arbeit zu einem
einheitlichen
Aggregat
Arbeit zusammengefaßt werden kann.
2. Die
Produktionsfunktion
Eine Produktionsfunktion gibt die bei gegebenem
technischen und organisatorischen
Wissen bestehende funktionale Beziehung zwischen
dem Volumen der effizient eingesetzten
Produktionsfaktoren ( hier Arbeit und
Sachkapital) und dem damit erreichbaren
Output wider.
Man unterscheidet zwischen substitutionalen
und limitationalen
Produktionsfunktionen (s. „Das
gesamtwirtschaftliche Multiplikatormodell“, W. Fuhrmann, A. Sultanow, in:
www.nowgorod.de).
Bei substitutionalen
Produktionsfunktionen kann die Produktion
bei gegebener, im
Produktionsprozeß eingesetzter Menge eines Faktors erhöht werden, wenn
die eingesetzte Menge
des anderen Faktors zunimmt bzw. es kann die gleiche Menge an Gütern mit
unterschiedlichen
Faktoreinsatzkombinationen produziert werden.
Bei limitationalen Produktionsfunktionen existiert dagegen für jeden
Output nur ein
effizientes Faktoreinsatzverhältnis bzw. nur eine Technologie.
2.1. Zur substitutionalen Produktionsfunktion
Eine substitutionale Produktionsfunktion
läßt sich grundsätzlich in der folgenden Form schreiben:
mit:
K Anzahl der im Produktionsprozeß eingesetzten
Sachkapitaleinheiten,
N Anzahl der im Produktionsprozeß
eingesetzten Arbeitsstunden oder
Humankapitaleinheiten.
Aufgrund der unterstellten Substitutionalität der Produktionsfaktoren gilt für diese
funktionale Beziehung:
Es führt der erhöhte Einsatz eines
Produktionsfaktors c. p. zu einem erhöhten Output: Die erste Ableitung des
Güterangebotes nach diesem Faktor ist positiv. Die
Grenzproduktivität dieses Faktors sinkt allerdings mit steigender Einsatzmenge.
Entsprechend ist die zweite Ableitung negativ.
Der Stand des
organisatorischen und technischen Wissens spiegelt sich in der jeweiligen Form
der Verknüpfung wider. Dieses Wissen wird hier als konstant unterstellt, d. h.
es gibt annahmegemäß keinen technischen Fortschritt.
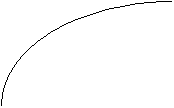
Für eine substitutionale
Produktionsfunktion ergibt sich die folgende graphische Darstellung des
Zusammenhanges zwischen Arbeitsmenge und Output bei gegebener Menge des Faktors
Sachkapital:
y
K1
K1 > K0
K0
0 N
Die Beziehung zwischen Produktion und
Arbeitseinsatz.
Jede Erhöhung des
Sachkapitalbestandes bedeutet eine Verschiebung dieser Kurve nach oben und
bedeutet gleichzeitig bei gegebener Beschäftigung eine Zunahme der
Grenzproduktivität der Arbeit, d.h. einen höheren Wert der ersten Ableitung des
Outputs nach dem Produktionsfaktor Arbeit: Die Kurve OK1 in der Abbildung weist bei jeder Beschäftigung eine
größere Steigung als die Kurve OK0
auf.
Weiterhin steigt mit dem
Kapitalstock die durchschnittliche Arbeitsproduktivität,
die als der Quotient von Output und Arbeitseinsatz definiert ist. Entsprechend
sinkt der Arbeitskoeffizient, der die im Durchschnitt eingesetzte Arbeitsmenge
pro Outputeinheit mißt und damit gleich dem reziproken Wert der durchschnittlichen
Arbeitsproduktivität ist.
Im Rahmen der kurzfristigen
Analyse wird unterstellt, daß der Sachkapitalbe-
stand exogen ist, so daß weder
der technische Fortschritt noch der Kapazitätseffekt der Investition im Modell
und damit in der Erklärung berücksichtigt werden.
2.1.1. Zur Cobb-Douglas-Produktionsfunktion
Zur Verdeutlichung der
produktionstheoretischen Zusammenhänge wird
kurz die
Cobb-Douglas-Produktionsfunktion
dargestellt. Diese Funktion lautet in ihrer allgemeinen Form:
mit:
(partielle) Produktionselastizität des Faktors Arbeit,
(partielle) Produktionselastizität des Faktors Kapital,
Rate des technischen
Fortschrittes pro Zeiteinheit.
Existiert annahmegemäß kein technischer Fortschritt, so gilt:
Der Exponent 
(
) gibt die partielle Produktionselastizität des
Faktors Arbeit (Kapital), d.h. die relative Veränderung des Outputs in
Abhängigkeit von der sie bedingenden relativen Veränderung der Einsatzmenge der
Arbeit (des Kapitals) an.
Ist die Summe der beiden
Exponenten gerade gleich eins, so ist das Niveaugrenzprodukt konstant, d.h. eine
prozentuale Veränderung der Einsatzmenge beider Faktoren (z.B. um das
) führt zu einer gleich großen prozentualen Veränderung von y:
bzw.:
Die
Cobb-Douglas-Produktionsfunktion ist also für den Fall, daß die Summe der
partiellen Produktionselastizitäten gleich eins ist, linear homogen. Bei einer
unterstellten Entlohnung der Faktoren nach ihren Grenzproduktivitäten (vgl. die
produktivitätsorientierte Lohnpolitik) kennzeichnen die Elastizitäten zugleich
die Einkommensverteilungen in der Volkswirtschaft: Die
Lohnquote beträgt 
, die Gewinnquote l - 
.
2.2.
Zur limitationalen Produktionsfunktion (Leontief-Produktionsfunktion)
Eine limitationale
Produktionsfunktion ist dadurch gekennzeichnet, daß es für
jede Produktionsmenge nur ein
Verhältnis der Produktionsfaktoren gibt, mit dem
dieser Output effizient
erzeugt werden kann. Dieses Einsatzverhältnis muß zwar bei variierender
Outputmenge nicht konstant sein, zur Vereinfachung wird jedoch häufig diese
zusätzliche Annahme getroffen und man erhält eine linear-limitationale
Produktionsfunktion. Die allgemeine Formulierung einer solchen
linear-limitationalen Produktionsfunktion
(Leontief-Produktionsfunktion) lautet:
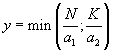
mit:
а1 (konstanter)
Arbeitskoeffizient,
a2 (konstanter)
Kapitalkoeffizient.
Bei gegebener Menge der
Produktionsfaktoren ist der Output somit gleich dem Wert des kleineren der in
der Klammer enthaltenen Inputkoeffizienten. Der dazugehörige Produktionsfaktor
ist der „Engpaßfaktor", der andere Faktor existiert im „Überfluß".
Die Einsatzmengen der
Produktionsfaktoren bestimmen sich aus den Faktorkoeffi-
zienten und der geplanten
Produktion.
3. Der Arbeitsmarkt bei Mengenanpasserverhalten
3.1. Die Arbeitsnachfrage
Um die gesamtwirtschaftliche
Nachfragefunktion nach Arbeit aus dem einzelwirtschaftlichen Kalkül einzelner
Unternehmungen abzuleiten, wird zur Vermeidung von Aggregationsproblemen wieder
ein sog. repräsentatives Unternehmen unterstellt. Für alle homogenen
Unternehmungen gilt somit die gleiche Produktionsfunktion, alle Unternehmungen
führen das gleiche Optimierungskalkül durch.
Der erwartete Gewinn ergibt
sich definitionsgemäß aus der erwarteten Differenz zwischen dem Umsatz und den
Kosten (im Gleichgewicht der vollkommenen Konkurrenz gilt G = 0):
mit:
G erwarteter (Nominal-) Gewinn,
p Güterpreis,
geplante Produktion (= Güterangebot),
W Nominallohnsatz
pro Arbeitseinheit,
NN geplante nachgefragte Arbeitsmenge,
i Zinssatz,
pK Preis
einer Sachkapitaleinheit,
K Anzahl
der im Produktionsprozeß eingesetzten Sachkapitaleinheiten,
ipK Kapitalkosten
pro Kapitaleinheit bei Vernachlässigung von Abschreibungen
Unterstellt
man, daß die Unternehmung die tatsächlichen Preise (p, pK ,W, i)
kennt bzw. korrekt erwartet und sich als Mengenanpasser verhält, so ergibt sich
bei gegebenem Kapitalstock die gewinnmaximale Nachfrage nach Arbeit aus der
nach dem Faktor Arbeit differenzierten Gewinngleichung:
Damit gilt für das Gewinnmaximum:
mit:
w (erwarteter)
Produzentenreallohnsatz.
Der
Quotient aus dem Nominallohnsatz und dem Güterpreis stellt den Produzentenreallohnsatz w dar. Der Lohnsatz ist nicht in Geld-,
sondern in Gütereinheiten ausgedrückt. Die Bedingung besagt somit, daß die
Unternehmung solange Arbeitskräfte nachfragen wird, bis die (mit zunehmender
Beschäftigung sinkende) Grenzproduktivität der Arbeit dem Reallohnsatz
entspricht.
Steigt
der Reallohnsatz infolge eines steigenden Nominallohnsatzes oder eines
reduzierten Güterpreises, so wird der für die letzte bisher eingesetzte Arbeitseinheit
zu zahlende Reallohnsatz größer als das Grenzprodukt dieser Einheit.
Entsprechend wird die Unternehmung den Arbeitseinsatz und damit auch die
Produktion bzw. das Güterangebot soweit reduzieren, bis die bei geringerem
Arbeitseinsatz höhere Grenzproduktivität das Niveau des Reallohnsatzes erreicht
hat. Die Nachfrage nach Arbeit sinkt somit bei gegebener Produktionsfunktion
mit steigendem Reallohnsatz.
Aufgrund der Annahme
repräsentativer bzw. homogener Unternehmungen gilt nicht nur
für jede einzelne
Unternehmung, sondern auch für die gesamte Volkswirtschaft, daß die
Arbeitsnachfrage mit steigendem Reallohnsatz sinkt:
Zur Verdeutlichung soll dieser Zusammenhang für ein Mengenanpasserverhalten an der oben
beschriebenen Produktionsfunktion vom Cobb-Douglas-Typ dargestellt werden. Aus
der ersten Ableitung der Gewinndefinition
nach dem Faktor Arbeit unter
Beachtung der Nebenbedingung in Form der Produktionsfunktion
folgt unmittelbar:
Setzt man diese erste
Ableitung gleich Null und löst sie nach der Arbeitsnachfrage
auf, so erhält man als
Nachfragefunktion nach Arbeit:
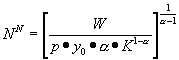
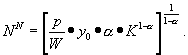
Das Beispiel verdeutlicht, daß
die nachgefragte Arbeitsmenge bei gegebenem Kapitalstock und technischem Wissen
mit steigendem Reallohnsatz sinkt. Ein steigender Kapitalbestand führt bei
gegebenem Reallohnsatz zu einer erhöhten geplanten Produktion (Mengenanpasser!)
und zu einer Zunahme der Arbeitsnachfrage, da ein steigender Kapitaleinsatz die
Grenzproduktivität der Arbeit erhöht. Bei gegebener Produktionsmenge führt
dagegen ein steigender Kapitalstock zu einer sinkenden Arbeitsnachfrage, wobei
allerdings zusätzliche Mechanismen aufgezeigt werden müssen, die die
Unternehmung trotz Erfüllung ihres Gewinnmaximierungskalküls zu einer solchen
Handlungsweise veranlassen sollten (z. B. sinkende Finanzierungskosten).
3.2.
Das Arbeitsangebot
Die Ableitung der
Angebotsfunktion auf dem Arbeitsmarkt erfolgt in Anlehnung
an ein sehr stark vereinfachtes
Optimierungskalkül der einzelnen Wirtschaftssubjekte. Jedes Wirtschaftssubjekt
hat eine Nutzenfunktion, in die als Argumente die Freizeit (F) und die verfügbaren Konsumgüter (c) eingehen (vereinfachend wird eine Sparquote von Null
unterstellt,
anderenfalls sind c und
das reale Vermögen v sowie F oder N Argumente der Nutzenfunktion):
Die Verfügungsgewalt über
Konsumgüter erhält das Wirtschaftssubjekt durch das über den Arbeitseinsatz
erzielte Einkommen. Dabei wird hier zur Vereinfachung außerdem unterstellt, daß
dieses Wirtschaftssubjekt kein Vermögen in Form von Aktien, Geld oder
Wertpapieren besitzt (dann gilt: 
).
Bei der Maximierung seines
Nutzens hat das Wirtschaftssubjekt die Zeitrestriktion zu beachten, also die
Tatsache, daß es für eine bestimmte Planungsperiode wie beispielsweise einen
Tag, nur über eine bestimmte Anzahl von Zeiteinheiten (wie beispielsweise 16
Stunden, bei 8 Stunden Schlaf) verfügen kann. Mit einer steigenden Anzahl von
Arbeitsstunden (N) verringert sich
also die Freizeit (F):
F=16 -
N.
Das Wirtschaftssubjekt hat
somit sein Optimum so zu bestimmen, daß das Grenzleid der Arbeit in Form von
Verzicht auf Freizeit 
gerade gleich dem Grenznutzen der Arbeit 
in Form
von verfügbaren Konsumgütern ist.
Je höher also der erwartete
Konsumentenreallohnsatz ist, um so höher ist der Grenzertrag einer
Arbeitsstunde und um so höher ist damit die angebotene Arbeitsmenge. Dies ist
der so genannte Normalfall.
Die Zunahme des
Arbetsangebotes ist bei einer Erhöhung des erwarteten Reallohnsatzes um so
niedriger, je geringer die Freizeit des Wirtschaftssubjektes bereits ist, da
der Grenznutzen mit sinkender Freizeit überproportional steigt. Entsprechendes
gilt für den Grenznutzen der verfügbaren Güter. Die ersten (zweiten)
Ableitungen der Nutzenfunktion sind positiv (negativ).
Auch bei diesem Verlauf der
Nutzenfunktion ist es nun allerdings in extremen Situationen durchaus denkbar,
daß mit steigendem erwarteten Reallohnsatz das Arbeitsangebot nicht steigt,
sondern fällt: Die Einkommensveränderung setzt sich ja aus der Veränderung des
erwarteten Reallohnsatzes und der Änderung der Beschäftigung zusammen. Bei
steigendem erwarteten Reallohnsatz führt also selbst eine (unterproportionale)
Reduktion des Beschäftigungsvolumens noch zu steigen den Einkommen. Ist der
Reallohnsatz relativ hoch, damit der Grenznutzen des zusätzlichen Einkommens
relativ gering, dann kann eine Reduktion der Arbeitszeit bei steigendem
Reallohnsatz sowohl Einkommen als auch Freizeit erhöhen. Der damit gewonnene
Nutzenzuwachs kann größer sein als der Nutzenzuwachs bei erhöhter Arbeitszeit und
reduzierter Freizeit. In diesem Falle hätte die Arbeitsangebotsfunktion in Abhängigkeit vom erwarteten
Reallohnsatz eine negative Steigung.
In der folgenden Analyse wird
jedoch nur der „Normalfall" eines mit steigendem erwarteten Reallohnsatz
steigenden Arbeitsangebotes und allenfalls noch der Grenzfall, in dem das
Arbeitsangebot unverändert bleibt, betrachtet. Damit folgt für die
Arbeitsangebotsfunktion:
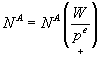
bzw.:
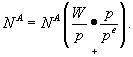
In der zweiten Formulierung dieser Funktion wird das Arbeitsangebot durch den tatsächlichen Reallohnsatz und die Relation zwischen tatsächlichem und erwarteten Güterpreis bestimmt. Dieser zweite Bestimmungsfaktor drückt den Erwartungsffehler der Konsumenten bezüglich der Güterpreise bzw. den Grad der Geldillusion bei den Haushalten aus. Unterstellt man, daß die Haushalte nicht nur den Nominallohnsatz, sondern auch den Güterpreis kennen bzw. richtig erwarten, so wird dieser Quotient gleich eins. In allen anderen Fällen unter- oder überschätzen sie ihren tatsächlichen Reallohnsatz. Dieser Zusammenhang wird in der folgenden Abbildung dargestellt:
N
N
NA
Die
Arbeitsangebotsfunktion.
Bei einem Erwartungsfehler von
Null (p = pe) ergibt sich
beispielsweise die Kurve NA0;
sie verschiebt sich bei gegebenem Nominallohnsatz mit steigender Unterschätzung
des Güterpreises nach rechts. Dabei ist jedoch zu berücksichtigen, daß aufgrund
der Beschränkung des Zeitbudgets eine bestimmte Obergrenze nicht überschritten
werden kann.
Schließt man wieder von dem
einzelnen (repräsentativen) Wirtschaftssubjekt auf
die Gesamtheit aller
Wirtschaftssubjekte und vernachlässigt damit die Aggregationsprobleme, so gilt
der in der obigen Abbildung dargestellte
Verlauf auch für das gesamte Arbeitsangebot einer Volkswirtschaft.
Alternativ zu der
dargestellten Reallohnabhängigkeit des Arbeitsangebotes wird verschiedentlich
in kurzfristigen Modellanalysen von vereinfachenden Annahmen ausgegangen:
1. Das
gesamtwirtschaftliche Arbeitsangebot ist konstant und unabhängig von der
Höhe des Reallohnsatzes. Begründet wird diese Hypothese damit,
daß nur
wenige Arbeitnehmer die Möglichkeit haben, die Anzahl ihrer
Arbeitsstunden
frei zu bestimmen, aber grundsätzlich alle arbeiten müssen, um
ihren
Lebensunterhalt zu verdienen. Ebenso ist die Entscheidung, ob
zusätzliche
Familienmitglieder eine Arbeit aufnehmen sollen oder nicht, in
vielen Fällen
nicht von der Höhe des Reallohnsatzes abhängig.
Gegen diese Hypothese spricht, daß es eine
Variationsmöglichkeit des Arbeits-
kräfteeinsatzes in Abhängigkeit von der Höhe des
Reallohnsatzes z. B. in Form
von zu leistenden Überstunden gibt. Die in allen
Tarifverträgen für Überstunden
vorgesehenen höheren
Lohnsätze können ein Indiz für den in der ersten
Hypothese angenommenen positiven Zusammenhang zwischen
Reallohnsatz
und Arbeitsangebot sein:
Die Arbeitskräfte sind
demnach offensichtlich nur bereit, mehr als die tariflichen
Wochenstunden zu leisten, wenn ihnen
dafür ein höherer Reallohnsatz gezahlt wird.
Ob diese Tatsache allerdings als Abhängigkeit des
Arbeitsangebotes vom Reallohnsatz
interpretiert werden kann, hängt davon ab, ob die Entscheidung
zur Leistung von Überstunden
vom Arbeitsanbieter
freigetroffen werden kann.
2.
Das Arbeitskräfteangebot ist kurzfristig vollkommen
elastisch in Bezug auf den Nотinallohnsatz. Hinter dieser
Hypothese steht die Überlegung, daß Lohnverhandlungen im allgemeinen in
längeren Zeitabständen zwischen
Arbeitgeberorganisationen und Gewerkschaften erfolgen.
Vernachlässigt
man die Überstundenzuschläge, dann sind innerhalb dieser Periode die Arbeiter
bereit, im Bereich der tariflichen Arbeitszeit zum ausgehandelten
Nominallohnsatz jede beliebige Menge an Arbeit anzubieten. Erst bei den
nächsten Lohnverhandlungen werden die Gewerkschaften in ihren Forderungen die
herrschende Arbeitsmarktsituation berücksichtigen.
3.3. Angebot und Nachfrage auf dem
Arbeitsmarkt
Aus dem
Gewinnmaximierungskalkül der Unternehmungen und dem Nutzenmaximierungskalkül
der Haushalte folgt eine negative Abhängigkeit der Arbeitsnachfrage und eine
positive Abhängigkeit des Arbeitsangebotes vom Reallohnsatz:
w NN
NA
w1
N1
w0
w2 N2
NA, NN
Der Arbeitsmarkt
Bei dem Reallohnsatz w0 sind Angebot und Nachfrage nach Arbeit
einander gleich, es gibt keine unfreiwillige Arbeitslosigkeit. Es gibt keine
Variation des Reallohnsatzes, durch die eine höhere Beschäftigung erreicht
werden kann. Entsprechend wird eine derartige Situation als Vollbeschäftigung
definiert.
Im Prinzip kann bei dem
Reallohnsatz w0 auch
Arbeitslosigkeit existieren, die allerdings nicht aus einem Gesamtdefizit an
Arbeitsnachfrage gegenüber dem Arbeitsangebot resultiert. Es handelt sich dann
entweder um
- friktionelle
Arbeitslosigkeit oder
- strukturelle
Arbeitslosigkeit.
Die friktionelle Arbeitslosigkeit ergibt sich aus dem in einer
Volkswirtschaft ständig erfolgenden Arbeitsplatzwechsel einzelner Arbeitnehmer,
die in der Periode zwischen Beendigung ihres alten Arbeitsverhältnisses und
Beginn ihres neuen Arbeitsverhältnisses eine gewisse Zeit arbeitslos sind.
Die strukturelle Arbeitslosigkeit
entsteht aus regionalen, qualitativen und zeitlichen Unterschieden zwischen
der Struktur der Gesamtnachfrage nach Arbeit und der Struktur des
Gesamtangebotes. In beiden Fällen kann jedoch davon ausgegangen werden, daß der
Zahl der Arbeitslosen eine in etwa gleich große Anzahl offener Stellen
entspricht.
Bei dem Reallohnsatz w1
besteht dagegen ein
Überschußangebot an Arbeit (bzw. Arbeitslosigkeit bzw. Unterbeschäftigung) in
Höhe von N1. Man bezeichnet diese Arbeitslosigkeit auch als
klassische Arbeitslosigkeit. Eine solche Situation kann entstehen, wenn sich
der Nominallohnsatz, aufgrund welcher Einflußfaktoren auch immer, trotz des
bestehenden Überangebotes nicht reduziert und bei diesem herrschenden, exogen
gegebenen Nominallohnsatz die gesamtwirtschaftliche Nachfrage so gering ist,
daß sich auf dem Gütermarkt kein Preis einstellt, der zu dem Reallohnsatz w0 führt.
Bei dem Reallohnsatz w2 besteht eine Überschußnachfrage nach Arbeit in Höhe von N2. Eine solche Situation kann sich beispielsweise äußern in einer großen Zahl nicht besetzter Arbeitsplätze bzw. offener Stellen. Unterstellt man einen flexiblen Nominallohnsatz, so wird sich in beiden Ungleichgewichtssituationen der Nominallohnsatz bis zum gleichgewichtigen Lohnsatz ändern.
Im einfachsten Fall kann unterstellt werden, daß die Veränderung des Nominallohnsatzes eine Funktion der Überschußnachfrage auf dem Arbeitsmarkt ist:
mit:
dW absolute Veränderung des Nominallohnsatzes
in der Zeit.
Herrscht auf dem Arbeitsmarkt
Überschußnachfrage seitens der Unternehmungen,
so unterstellt diese
Anpassungshypothese, daß die Unternehmen in Konkurrenz
um den knappen Faktor Arbeit
den Nominallohnsatz nach oben konkurrieren. In
einer Situation des
Überschußangebotes dagegen konkurrieren die Arbeitskräfte
um die knappen Arbeitsplätze,
so daß der Nominallohnsatz sinkt. Dieser einfache
walrasianische
Anpassungsprozeß wird zumeist in der folgenden Form geschrieben:
mit:
prozentuale Veränderung des Nominallohnsatzes,
u Arbeitslosenrate 
Man bezeichnet diese Funktion
auch als „naive Phillips-Kurve".